Kondensaattori $C$

Kondensaattorin läpi ei kulje tasavirta, mutta smg-kenttä selviää, kuten on opiskeltu. Vaihtojännite $u(t)$ siis kulkeutuu kondensaattorin läpi. Yleisesti ottaen virta kondensaattorin läpi on suoraan verrannollinen jännitteen muutosnopeuteen, eli

$i = C \frac{dU}{dT}$.

Yksinkertainen C-virtapiiri on

Siinä kulkeva virta $i(t)$ on

$i(t) = C \frac{du}{dt} = C \frac{u_0\sin(2\pi ft + \phi_0)}{dt}$

$i(t) = Cu_0 2\pi f \cos(2\pi ft + \phi_0)$

Muutetaan kosini siniksi (muista matikka 9 -kurssista), saadaan

$i(t) = Cu_0 2\pi f \sin(2\pi ft + \phi_0 + \frac{\pi}2)$,

eli jännitteen ja virran välillä $\frac\pi2$ vaihe-ero. Virta $i(t)$ on edellä (koska $+$-merkki). Samalla nähdään, että jännitteen ja virran suhde on $\frac1{2\pi fC}$. Se on nimeltään reaktanssi, $X_C$:

$X_C = \frac1{2\pi f C}$

 

 

 Käämi eli kela $L$

Käämissä muuttuva sähkövirta aiheuttaa mg-kentän, joka puolestaan Lenzin lain mukaisesti vastustaa virran muutosta, eli

$u(t) = L \frac{di}{dt}$.

Yksinkertainen $L$-virtapiiri on

Tässä käämin yli oleva jännite $u(t)$ on

$u(t) = L \frac{di}{dt} = L \frac{i_0 \sin(2\pi f t + \phi_0)}{dt}$

$u(t) = L i_0 2\pi f \sin(2\pi f t + \phi_0)$

Muutetaan taas kosini siniksi, saadaan

$u(t) = L i_0 2\pi f \sin(2\pi f t + \phi_0 + \frac\pi2)$

Eli jännitteen ja virran välillä taas $\pi/2$:n vaihe-ero. Nyt virta on jäljessä. Huomataan, että jännitteen ja virran suhde on $L2\pi f$, ja sitä kutsutaan reaktanssiksi $X_C$

$X_C = 2\pi f L$.

Ohmin laki

Ohmin laki $R = \frac UI$ pätee myös vaihtovirtapiireille. Resistanssin $R$ paikalle kirjoitetaan impedanssi $Z$, joka määritellään

$Z = \sqrt{R^2 + (X_L – X_C)^2}$, jossa

vaihekulma $\phi = \arctan\left( \frac{X}{R} \right)$

Tämän perustelu on helppoa kompleksiluvuilla; reaktanssi $X = X_C – X_L$ on imaginaarinen ja resistanssi $R$ reaaliluku. Ne ovat kohtisuorassa toisiaan vasten (kompleksilukujen kurssi), joten pituus lasketaan Pythagoraan lauseella.

Teho vaihtovirtapiirissä; tehollinen arvo.

Hetkellinen teho on $p = u\cdot i$. Vastuksen yli $u = Ri$, eli saadaan $p = u\cdot i = R i^2$, kuten tasavirtapiirille.

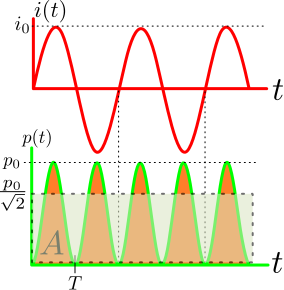
Sinimuotoinen teho on kuvaajasta katsottuna tällainen:

Yllä sinimuotoinen virta, alla sen neliö. Aktiivinen lukija huomaa, että $p_0 = Ri_0^2$. Teho siis vaihtelee vaihtovirtapiirissä ollen välillä jopa nolla. Keskimääräinen (ns. lämmittävä) teho saadaan integroimalla eli laskemalla vihreän käyrän alla oleva pinta-ala (ruskea) $A$ ajanhetkestä $0$ hetkeen $T=1/f $ [miksi?] jaettuna välin pituudella. Integrointi on helppo;

$ p_t = \frac AT = \frac1T \int_0^T p(t) $

$ p_t = \frac1T \int_0^T p(t) R (i_0 \sin(2\pi f t + \phi_0) )^ 2 dt$

Integroimalla ja sijoittamalla $T = 1/f$ paikalleen, saadaan

$p_t = \frac{R i_0^2}2= R \left( \frac{ i_0}{\sqrt2}\right)^2 $.

Siispä keskimääräistä tehoa vastaava keskimääräinen virta on $i_0/\sqrt2$, eli huippuarvo alle neliöjuuri kaksi. Sitä kutsutaan teholliseksi arvoksi.

Se vastaa siis suorakulmion, jonka pinta-ala on sama kuin sinikäyrän, korkeutta. Kuvassa katkoviivoitettu harmahtava laatikko.

Sama käsittely voidaan tehdä jännitteelle aivan vastaavasti. Siitä saadaan jännitteen teholliseksi arvoksi $i_t = i_0/\sqrt2$. Täysin vastaavasti.

Tehollinen teho on virran ja jännitteen huippuarvoista laskettuna

$P_t = u\cdot i = \frac{u_0 i_0}{\sqrt2 \sqrt2} = \frac{u_0 i_0}{2}$.

Näennäisteho, $S$

Yksikkö VA, volttiampeeri. Sisältää kompleksisessa mielessä pätö- ja loistehon. Siitä ei paljoa enempää.

Pätöteho, $P$

Yksikkö W, watti. Pätöteho kuluu piirissä.

Loisteho, $Q$

Yksikkö Var, vari. Loisteho ei kulu, “heilahtelee” edestakaisin. Yksinkertainen käsittely vaatii kompleksiaritmetiikan hallintaa.

Loistehoa aiheuttaa omgelmaa sähkönjakelussa, koska verkosta ei saada kaikkea mahdollista tehoa ulos; virta kasvaa liikaa. Suurasiakkaat joutuvat maksamaan loistehosta. Heillä on isoja sähkömoottoreita (käämejä), jotka “ottavat” loistehoa. Loisteho pyritään kompensoimaan, yleensä rinnakkaiskondensaattoreilla.

Tehokerroin

Tehokerroin $\cos\phi$ on pätötehon suhde loistehoon; täysin resistiivisellä kuormalla tehokerroin on $1$, muutoin pienempi.

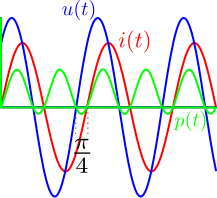
Kuvassa on sinimuotoinen jännite ja virta piirrettynä vaihe-erolla $\phi_0 = \pi/4$.

Vihreä tehokäyrä, eli jännitteen ja virran tulo on välillä negatiivinen. Se palauttaa tehoa järjestelmään. Siksi loisteho “heilahtelee” edestakaisin.

$|P| = |S| \cos\phi_0$.

Eri tehokomponenteille pätee vastaa Pythagoraan yhtälö kuin reaktansseille, eli

$S^2 = P^2 + Q^2 $.

J a t k u u . Tai sitten ei.