Kirjasta suoraan

Kolmion $OAB$ sivulla $AB$ on piste $C$ niin, että se jakaa sivun $AB$ suhteessa $2:1$. Missä suhteessa $B$:stä piirretty keskijana jakaa janan $OC$?

Tästä pitää pitää pystyä piirtämään allaoleva kuva. Ainoa ongelma on keskijana, mutta selvästi se ei voi tarkoittaa muuta kuin sitä ilmeistä.
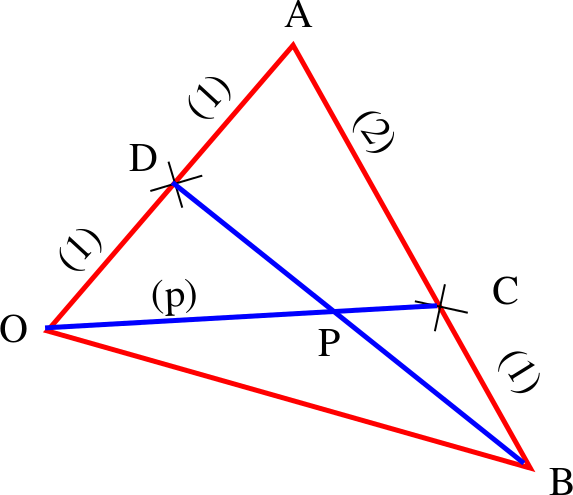Suhde $p$ on kysytty suure, ja sekin pitäisi osata laittaa paikalleen. Seuraavaksi kannattanee muodostaa yhtälöt noille kahdelle siniselle viivalle. Sitä varten muodostetaan muutama vektori; eli piirretään nuolet ja merkitään suuntajanat vektoreilla, esim. $\vec a$.

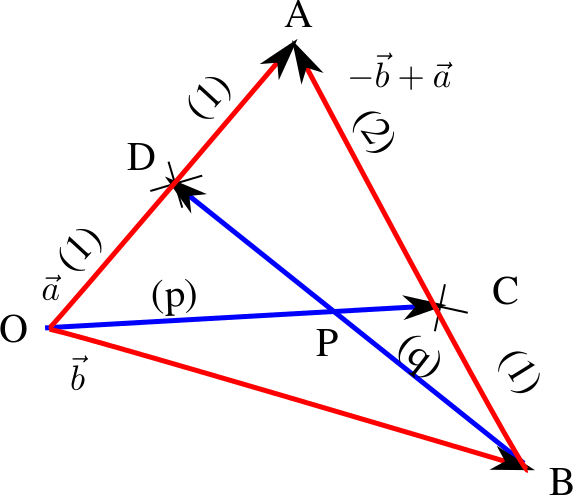Eli vektori $\vec a = \vec{OA}$, $\vec b = \vec{OB}$ ja kolmannelle saadaan selvästi (katso kuvasta) $\vec b – \vec a$. Huomaa strategisesti valitut suunnat (seuraavaa virkettä ajatellen). Sitten vain muodostetaan jakopistelauseen avulla vektorit

$\vec{OC}= \frac{2\vec b + \vec a}{3}$

$\vec{BD} = \frac{(-\vec b ) + (-\vec b+ \vec a)}{2} = \frac{\vec a – 2\vec b}2$.

Tässähän sen työ oli. Nyt pitää taas ottaa silmä päähän ja katsoa kuvaa. Nyt piti vain lisätä sinne suhde $q$. Se oli pieni hämy, mutta pakkohan se on.Selvästi

$\vec{OP} = p\vec{OC}$ ja

$\vec{OP} = \vec{OB} + \vec{BP} = \vec{OB} + q\vec{BD}$.

Ylempi on siis alempi, ja laitetaan aiemmin lasketut jakosuhdevektorit paikoilleen:

$p\vec{OC} = \vec{OB} + q\vec{BD}$

$p\frac{2\vec b + \vec a}{3} = \vec b + q\frac{\vec a – 2\vec b}2$.

Siis saadaan

$\vec a \left(\frac p3\right) +\vec b\left(\frac{2p}3\right) =\vec a \left(\frac q2\right) + \vec b \left(1-q\right)$

Vektoriesityksen yksikäsitteisyyden nojalla molempien vektorien kertoimet pitää olla samat:

$\frac p3 = \frac q2$

$\frac{2p}3 = 1-q$.

Yhtälöryhmästä saadaan ratkaisut $p=\frac34$ ja $q=\frac12$. Kysytyt suhteet olivat $p$ ja $1-p$ eli jakosuhde on $\frac34:\frac14$ eli $3:1$.