Todistetaan kosinilause

$c^2 = a^2 + b^2 – 2ab\cos\gamma$

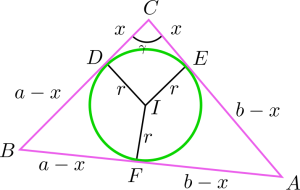
kolmion sisään piirretyn ympyrän avulla. Olkoon $ABC$ mielivaltainen kolmio, jonka sisällä oleva $r$-säteinen ympyrä sivuaa sitä pisteissä $D$, $E$ ja $F$. Olkoon vielä kulma $\gamma$ pisteestä $C$ aukeava kulma $\gamma = ACB$.

Olkoon $x=CD=CE$ (miksi?). Merkitään alla olevan kuvan mukaisesti janan $c$ pituudeksi $AB$ on $c =AB= (a-x)+(b-x)$, josta saadaan

$x = \frac{a+b-c}{2}$.

Kolmio $CEI$ on suorakulmainen, ja siitä saadaan puolikas $\gamma$. Selvästi

$\tan \frac\gamma2 = \frac rx$ eli $x = \frac r{\tan \frac \gamma2}$.

Yhdistetään kaksi lauseketta $x$:lle ja saadaan

$\frac{a+b-c}{2} = \frac r{\tan \frac \gamma2}$ josta

$r = \frac{a+b-c}{2}\tan\frac\gamma2$.

Lasketaan kolmion $\Delta ABC$ pinta-ala kahdella eri tavalla saadaan

$\frac12ab\sin\gamma$ ja

$\frac12r(a+b+c)$ (taulukkokirjasta: sisään piirretyn ympyrän säde).

Ratkaistaan näistä pinta-aloista $r$ ja saadaan

$r=\frac{ab\sin\gamma}{a+b+c}$.

Sitten samaistetaan nämä kaksi eri lauseketta $r$:lle ja saadaan

$\frac{a+b-c}{2}\tan\frac\gamma2=\frac{ab\sin\gamma}{a+b+c}$

Kerrotaan oikean puolen jakaja pois ja jaetaan vasemman $\tan$-termillä, jolloin saadaan (miksi?)

$(a+b)^2 – c^2 = 2ab\frac{\sin\gamma}{\tan\frac\gamma2}$

Siirretään vielä $(a+b)^2$ toiselle puolella, poistetaan siitä potenssi ja kerrotaan vielä $-1$:llä

$c^2 = a^2+b^2+ 2ab  – 2ab\frac{\sin\gamma}{\tan\frac\gamma2}$

$c^2 = a^2+b^2+ 2ab  – 2ab\sin\gamma\frac{\cos\frac\gamma2}{\sin\frac\gamma2}$

Eli ilmaistiin tangentti sinin ja kosinin avulla. Seuraavaksi muistellaan (taulukkokirjasta), että $\cos^2 x = \tfrac12(1 + \cos 2x)$. Siis yritetään muuttaa trigonometriset funktiot puolikkaiksi. Ensin kaksinkertaisen kulman tulos sinille:

$\sin\gamma\frac{\cos\frac\gamma2}{\sin\frac\gamma2}$

$=2\sin\frac\gamma2\cos\frac\gamma2\frac{\cos\frac\gamma2}{\sin\frac\gamma2}=2\cos^2\frac\gamma2$

ja näyttää hyvältä! Dumpataan tuo alkuperäiseen yhtälöön. Saadaan:

$c^2 = a^2+b^2+ 2ab  – 2ab 2\cos^2\frac\gamma2$

$c^2 = a^2+b^2+ 2ab(1  – 2\cos^2\frac\gamma2)$

Tuohon vielä aiemmin mainittu kosinin neliösääntö, niin

$c^2 = a^2+b^2+ 2ab(1  – 2\tfrac12(1 + \cos 2\frac\gamma2))$

$c^2 = a^2+b^2+ 2ab(1 -1- \cos \gamma)$

$c^2 = a^2+b^2- 2ab\cos \gamma$

 qed.